| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 프로바이오틱스
- DataProcessing
- 프레딧
- NLinear
- 오토트레이딩
- MPRO
- node.js
- ML
- 엠프로
- express
- 흥미붙이기
- YOLO
- pandas
- DL
- 강화학습으로주식하기
- LTSF
- RL
- 벨만방정식
- socket.io
- 도커로 깃블로그 만들기
- 강화학습
- HY7714
- 불법마약특별단속 #부산지방경찰청
- mlflow
- AI
- 제발쉽게좀가르치자
- transformer
- DLInear
- de
- TimeSeries
- Today
- Total
상황파악
파이썬과 케라스로 배우는 강화학습 #2. MDP와 벨만 방정식 본문
MDP 구성요소
이전 내용에서 MDP 구성요소로 상태,행동,보상을 설명했다.
조금 더 자세히 설명하자면 상태, 행동, 보상함수, 상태 변환 확률, 감가율 총 5개의 요소로 구성되어 있다.
상태 (State)
상태와 행동은 에이전트가 현재 환경안에서 어떤 상태에 놓여있는지 (위치는 어디인지, 지금 어디로 이동하고 있는지, 주변에 바람은 어떻게 부는지 등) 같은 관찰 가능한 상태의 집합 (S) 이다.

책에서 설명하는 예시를 가져왔다
그리드월드에서 상태값은 좌표값이다. (왜 (1,1) 우측이 (1,2) 가 아니라 (2,1) 인지는 모르겠다)
5x5 행렬이 있다고 했을 때, 그리드월드의 상태 집합은 S=(1,1),(1,2),(1,3),...,(5,5) 로 표시할 수 있다.
에이전트는 시간에 따라 25개의 상태의 집합 안에 있는 상태를 탐험하게 된다.
시간 t 일때의 상태는 St 로 나타낸다. 현재 빨간 사각형의 초기 위치는 s0=(1,1) 이다.
행동 (Action)
에이전트가 상태 St에서 할 수 있는 가능한 핸도으이 집합 A
보통 에이전트가 할 수 있는 행동은 모든 상태에서 같다.
위 예시에서 그리디월드 내 에이전트가 수행할 수 있는 행동은 A={up,down,left,right} 인 것이다.

보상 함수 (Reward Function)
환경이 에이전트한테 주는 보상값을 계산하는 함수.
Ras=E[Rt+1|St=s,At=a]
t 시점의 상태 St=s 에서 At=a 를 수행했을 때
(위 예시로 들면 (1,1) 에서 right 행동을 수행했을 때)
에이전트가 받을 수 있는 보상이 얼마인지에 대한 기대값을 계산해주는 것이 보상함수이다.
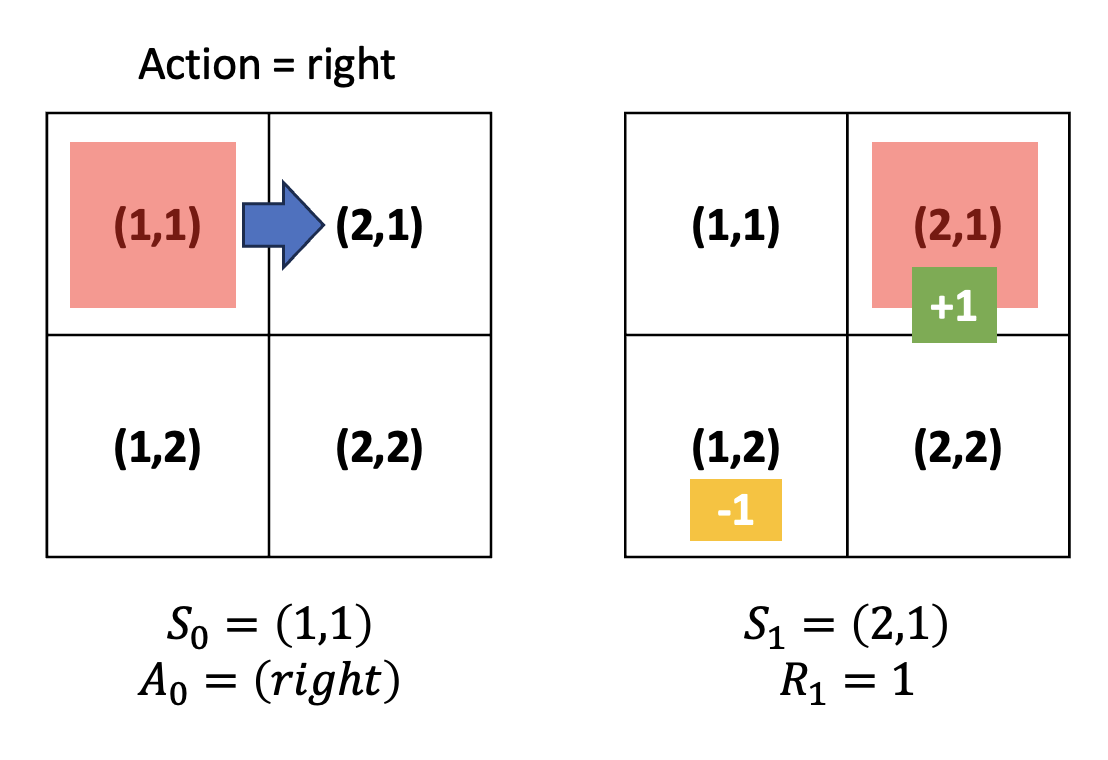
위 예시에서는 St 에서 Right 이라는 action을 했기 때문에 +1 이라는 보상을 얻은 것이고, 만약 Down 이라는 action을 했다면 -1의 보상을 얻었을 것이다.
기대값이란 무엇이고, 왜 기대값을 사용하는 걸까?
책의 설명을 빌리자면 기대값이란 일종의 평균이다.
예) 주사위를 굴렸을때의 기대값
기대값=1×16+2×26+3×36+4×46+5×56+6×66=216
이렇게 해석하는게 맞는지 모르겠지만 주사위를 굴리는 시도는 3.5 의 기대값을 가진다고 보인다.
이처럼 Agent 가 St 에 At 를 수행했을 때 보상함수는 받을 것이라 예상되는 숫자를 E(Expectation) 를 알려주고, 이를 통해 Agent 가 학습해가는 것이다.
왜 보상함수는 기대값으로 표현할까?
책에서는 '보상을 에이전트에게 주는 것은 환경이고, 환경에 따라서 같은 상태에서 같은 행동을 취하더라도 다른 보상을 줄 수도 있습니다' 라고 설명하고있다.
보상이라는 것은 에이전트가 판단하는 것이 아니라 환경이 알려주는 것이기 때문에 이 행동이 좋다 나쁘다를 알 수 없고,
어느정도 학습한 모델을 가지고 다른 상황에 두게 된다면 또 다른 결과가 나타날 수 있기때문에
이러한 모든것을 고려해서 보상함수를 기대값으로 표현한다고 한다.
나는 '환경에 따라 보상이 다르다' 라는 표현을 어드벤처 게임에서 문을 여는 행동을 스토리 진행을 위함이지만, FPS 에서 문을 여는 것은 총 맞을수도 있는 행동으로 이해했다.
특이한 점은 Ras 는 s 상태일때 a 라는 액션을 한다면 얻게되는 Rt+1(reward) 의 E(Expectation) 값을 알려주는 것이다.
t 시점이 아닌 t+1 시점이다.
행동을 한 시점과 보상의 시점이 다른 이유는 보상을 에이전트가 알고 있는 것이 아니고 환경이 알려주는 것이기 때문이다.
상태 변환 확률
사실 상태가 변한다는 것은 에이전트가 수행한 행동이 온전히 이루어 졌을때를 가정한다.
하지만 현실처럼 변수가 많은 환경이라면 내가 수행하고자 하는 동작이 100% 생각대로 이뤄지지 않을 수 있다.
이런 부분을 고려하는 것이 상태 변환 확률이다.
예를 들어 기철이는 집에 가야하는데 바람이 너무 강하게 불어 앞으로 가기도 힘든 상황이라면, 우리가 상상했던 집에 도착한 상태가 되기 위해 1초 뒤 앞으로 한걸음 나아간다 라는 행동이 온전히 이뤄지지 않을 수 있다는 것이다.

이를 수식으로 표현했을 때 아래와 같이 나타낼 수 있다
PaSS′=P[St+1=s′|St=s,At=a]
t 시점인 상태 s에서 a 를 수행했을 때, t+1 시점에 S′으로 변할 확률을 PaSS′로 나타낸 것이다.
감가율 (Discount Factor)
할인율이라고도 불리는 감가율의 개념은 동일한 의미를 지닌다
돈의 가치는 시간에 따라 다르다.
미래의 가치는 현재의 가치보다 낮을 수 밖에 없다.
그렇기에 가치를 일정부분 충당하기 위해 은행에서는 예금이자라는 방식으로 운용을 하고있다.
보상역시 비슷한 개념으로 작용한다.
내가 너무 배가고파 쓰러질 지경이라면, 당장 라면을 끓이기 위해 냄비 하나만 빠르게 씻는게 모든 설거지를 한번에 다 끝내고 물을 올리는 것 보다 보상이 큰 행동일 것이다.
즉, 같은 보상이라면 시간이 지날수록 가치가 줄어든다는 것이다.
감가율은 γ [감마] 로 표현하고, 0 ~ 1 사이의 값을 가진다 (시간이 지날수록 줄어들어야 하니까 1보다 크면 안되고, 0보다 작으면 보상의 크기를 계산하는 문제가 아니게 된다)
γ∈[0,1]
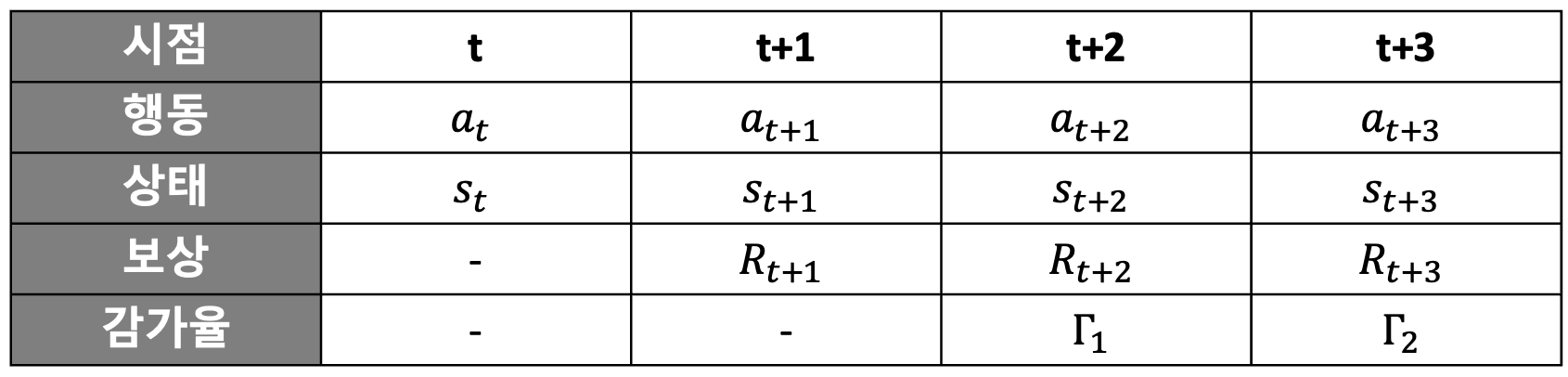
현재 시점 t 로부터 k 가 지난 후의 보상을 Rt+k 라고 했을때 감가율을 고려한다면 이렇게 표현할 수 있다
γk−1Rt+k
정책
모든 상태에서 에이전트가 할 행동
벌써부터 머리가 아프다
상태는 π 로 나타내고, Input:s(상태)→Output:a(행동) 인 일종의 함수다
책에서는 이렇게 설명한다
에이전트가 강화핛브을 통해 학습해야 할 것은 수많은 정책 중에서 최적 정책입니다. 최적 정책은 각 상태에서 단 하나의 행동만을 선택합니다. 하지만 에이전트가 학습을 하고 있을 때는 정책이 하나의 행동많을 선택하기 보다는 확률적으로 여러 개의 행동을 선택할 수 있어야 합니다.
에이전트가 할 수 있는 액션들은 (보편적으로) 이미 정해져있다. 내가 (3,4) 위치에서 위로 가야할지, 아래로 가야할지, 어디로 가야하는지를 이미 계산이 되어 있다는 것이다.
강화학습을 위해선 모든 것이 다 수식으로 정의가 되어야 모델이 학습할 수 있기 때문에 정책 역시 수식으로 표현이 가능하다.
π(a|s)=P[At=a|St=s]
이 수식을 책에서는 이렇게 표현한다
시간 t에 St=s 에 에이전트가 있을 때 가능한 행동 중에서 At=a 를 할 확률을 나타냅니다
그러니까 내가 (3,4)에서 각 행동별로 어떤 행동을 할지 확률을 계산한다는 것이다.
Up일 확률 30% Down일 확률 15% Right일 확률 10% Left일 확률 45% 이런식으로
그렇다면 이 확률들은 어떻게 알 수 있었을까
바로 가치함수를 통해 알게되는데, 가치함수는 받을 것이라 예상하는 보상을 알려주는 역할을 한다.
가치함수 (Value Function)
다시 확인해야 할 부분을 짚어보자
- 보상은 t 시점에 a 액션을 한 이후, 환경이 알려주는 t+1 시점의 정보
- 즉, 시간 t에 대한 보상은 Rt+1
일련의 보상들을 단순하게 합하면 아래와 같다
Rt+1+Rt+2+Rt+3+Rt+4+RT+5+ ...
하지만 이전에 설명한 감가율 (Discount Factor) 이 고려되어야 시점에 대한 최선의 행동을 더욱 정확히 판단할 수 있게 된다.
감가율을 적용한 보상들의 합을 표시하면 아래와 같다
Rt+1+γRt+2+γ2Rt+3+γ3Rt+4+γ4Rt+5 ...
시점에 해당하는 감가율을 고려하여 합한 보상을 Gt (반환값, Return) 라고 한다
반환값을 수식으로 표현해보면 위 식을 그대로 사용한다
Gt=Rt+1+γRt+2+γ2Rt+3 ...
반환값 G는 에이전트가 실제로 환경을 탐험하며 받은 보상들을 정산한 것이다
예를들어 목표까지 t=1 에서부터 t=5 까지 총 5번의 step을 수행했다면 아래와 같이 표현할 수 있다
G1=R2+γR3+γ2R4+γ3R5+γ4R6 G2=R3+γR4+γ2R5+γ3R6 G3=R4+γR5+γ2R6 G4=R5+γR6 G5=R6
G1 값에 R2 부터 R6 까지의 값이 더해지는 이유는
총 5번의 step을 수행했기 때문에 나중에 정산하는 시점에서 살펴본 것이기 때문이다
아, 내가 t=1 일때 부터 t=5 일때 까지의 보상들을 더해보니 G1 이라는 값이 됐구나
(이때 감가율이 고려가 되고, 보상은 t+1의 값이니까 R6 까지 표현)
그리고 t=2 일때 부터 t=5 까지의 보상들을 더해보니 G2가 되었구나
이런식으로 계산을 한 것이다
이렇게 정산을 하는 방법은 step이 다 끝난 이후 (에피소드가 종료된 후) 알 수 있다 (뭔가 기존 ML의 Epoch 같은 느낌이 든다)
하지만 반드시 그럴 필요는 없다
정확한 데이터를 사용하는것은 좋지만, 경험해야 할 단계가 너무 많다면 조금 고민이 될 것이다
상대적으로 정확도가 낮더라도 현재의 정보를 토대로 행동하는 것이 나을 때가 있다
에이전트도 모든 상황을 직접 경험해서 보상을 받지 않더라도, 아 이상황에서는 이렇게 하면 보상을 어느정도로 받겠구나 라는걸 예측할 수 있다
정확히 말하자면 어떤 상태에 있으면 앞으로 얼마의 보상을 받을 것인지에 대한 기댓값을 고려해 볼 수 있습니다. 그것이 바로 가치함수입니다. 간단하게 기댓값은 반환값의 기댓값으로 표현됩니다.
v(s)=E[Gt|St=s]
v가 소문자인 이유는 확률변수가 아니라 특정 양을 나타내는 값이기 때문이다.
또한 가치함수는 에이전트가 가지고 있는 값이다.
그러니까 내가 배가 고픈상태인데, 배가 부르면 기분이 좋겠다 (보상) 라고 한다면 우리는 그 상태가 되기 위해 밥을 먹는 행동을 한다
물론 배가부르기 위해 지금 당장 밥 먹는게 잘못된 선택일 수도 있다.
책에서는 옷 쇼핑하는 예시를 들었다.
옷을 볼때도 괜찮을 것 같아서 샀지만 막상 입어보면 아닌 것 처럼 실패를 할 수 있다
하지만 고민하는 과정을 반복해서 하다보면 결국 기대가 정확해지기 때문에 괜찮다
에이전트 또한 가치함수를 통해 어떤 상태가 좋을지 판단한다
앞으로 받을 보상에 대한 기댓값인 가치함수는 아래 수식으로 표현할 수 있다
v(s)=E[Rt+1+γRt+2+γ2Rt+3 ...|St=s]
이 식(가치함수)을 반환값 G의 형태로 표현하면
v(s)=E[Rt+1+γ(Rt+2+γRt+3 ...)|St=s]
v(s)=E[Rt+1+γGt+1|St=s]
t 시점의 보상은 Rt+1 인 것을 기억하자
여기서 한가지 고민해야 할 부분은 Gt+1=Rt+2+γRt+3 ... 인 부분인데,
G는 실제로 단계를 진행해보고 알게된 보상값들의 정산이라고 했지만 이 식에서는 예상값 (기대값) 이다
그렇기 때문에 앞으로 받을 보상에 대한 기댓값인 가치함수로 표현할 수 있다
Gt+1→v(St+1)
v(s)=E[R+t+1+γv(St+1)|St=s]
현 시점의 가치함수를 다음 시점의 가치함수로 표현하는 것을 보니 무한급수 같은 느낌도 든다
위 수식은 정책을 고려하지 않은 기대값이다
내가 지금 사용하고 있는 정책을 접목했을때의 예상 기대값을 표현하면
vπ(s)=Eπ[Rt+1+γvπ(St+1|St=s]
바로 벨만 기대 방정식 (BellmanExpectationEquation) 이 된다
저자는 이 식을 아래와 같이 표현했다
벨만 기대 방정식은 현재 상태의 가치함수 (vπ(s)) 와 다음 상태의 가치함수 (vπ(St+1) 사이의 관계를 말해주는 방정식입니다. 강화학습은 벨만 방정식을 어떻게 풀어나가느냐의 스토리입니다.
'AI > 강화학습' 카테고리의 다른 글
| [Q-learning] 데이터로 설명하기 (0) | 2024.01.09 |
|---|---|
| Toy Proj. 강화학습으로 주식하기 (1) | 2023.12.28 |
| 제발 좀 쉽게 가르치자 - 강화학습 1편 (0) | 2023.10.09 |
| 파이썬과 케라스로 배우는 강화학습 #1. 개요 (0) | 2023.08.26 |




